Pattern Recognition is a function that we all perform. In asking how to do it by computer we need consider at least three different approaches, fundamental concerns regarding the actual process: Statistics, Learning, and Structure. Further, two terms play important roles in practice: Features and Classification Decisions. Specialized subdisciplines have emerged in the research literature on patterns. The most important are Vision, Understanding, and Speech. Linguistic topics, e.g., Signs and Characters (Letters, Numbers), exemplify how basic notions extend into research and applications.

Patterns have a history in computer systems. Although that involved some change over time, the computer community has been in agreement on two things: a working definition, and the relation of the pattern recognition function to creating artificial intelligence. Here's the definition [1]: A pattern is an element from a set of objects that can in some useful way be treated alike. Next, there are five areas where improved computation is needed to create artificial intelligence [1]. At least three of them, Search, Learning, and Pattern Recognition, are part of the material we discuss here. (The other two are Planning, and Induction.)

Words describe patterns and actions. For example, most know immediately what the descriptive phrase "big dipper" indicates about a region of the night sky. Terms like symmetric, irregular heart beat, and constellation all indicate a pattern-property. (But even natural systems without language such as bees can recognize whether a flower is symmetric or not.) Still computers operate on numeric data, so a fundamental activity in this area is mapping a description (which may also be given by words) into a numeric representation.

Some fields of learning depend heavily on past Pattern Analysis activity. One form is the link between currently observable events and future consequences (e.g., Medicine associates diagnoses to symptoms). Another is a labeling, naming, or concept-identification approach. For instance, Mathematics places labels about properties on general cases. It extrapolates the characteristic from specific instances (e.g., odd from {1, 3, 5, 7}). The sum of that activity is a group of related concepts. Some of those are essential in general: set, subset, natural numbers (namely {1, 3, 5, 7, ...}). While Pattern Analysis could be discussed in terms of abstract concepts, it is such a common human activity that we focus instead on the process. There assigning, labeling, and grouping are basics.

For our common understanding of the Pattern Analysis process we seek to extend what is done to systematize knowledge in Medicine, Astronomy, Chemistry, Biology and many other fields. Generalization from specific characteristics is one of several activities. Another is deciding that there are so many differences between items that they must be considered dissimilar. (Examples: apples and oranges; cats and dogs; day and night.) Once the focus shifts to difference instead of commonalities (fruit; mammalian; part of a day) we are defining one or more set membership properties.

Another common activity passes on accumulated knowledge. Models and systems to replicate in computer programs training of new experts starts algorithmic, hardware-design, statistical, and psychological activities involving patterns.

Two idealizations of the human pattern process could be described as:

1. learning process; and,
2. training experts (or computer programs)

1. What number should follow 24 in:
   
   10, 11, 12, 13, 14, 15, 16, 17, 20, 22, 24, __?


2. Arrange eight coins in two straight lines each containing five.



3. (Based on Polya [2, p. 89]) Seven of the twenty-six capital Roman letters follow: (I.) A, M, T, U, V, W, and Y. If this is the first of five groups of letters, and each list of letters describes a set with general attributes that differ from the others, what distinguishing characteristic or feature defines this one in contrast with the others? The other groups that exhaust the remaining Roman capital letters are:
   II. B, C, D, E, K;
   III. N, S, Z;
   IV. H, I, O, X; and,
   V. F, G, J, L, P, Q, R.
   

[5, 6]. The third problem shows that an abstract notion like symmetry can be the basis of classification. Here the author of that question went beyond the vertical and horizontal symmetries. (In vertical symmetry replacing x by -x leaves y unchanged. Horizontal symmetry has no change in x when y is replaced by -y.) Adding central symmetry (where substitution of -x for x leads to the new value -y in place of the prior one, y) makes it possible to add several other classes. One has central occuring, and only that kind of symmetry. Another corresponds to situations where all these three symmetries are present. Finally there is a fifth category where no symmetry occurs.

Structure is a major consideration in its own right. In practice it plays a major role in assigning patterns to classes. The reason the second problem presents a challenge is that the solution depends on perceiving that structure is an intrinsic aspect of possible responses.

Direct and Informative

In some cases the pattern is perceived through directly viewing something but in others that is not true. Electrocardiograms have observable peaks and valleys but electroencephlograms differ when viewed even though their Fourier transforms may have similar frequencies and amplitudes at them. Likewise some informative patterned data may be extremely sparse in features. A good example is the absence of enclosed regions in alphabetic letters written in the horizontal dashed line font characterizing an IBM logo.

Two figures drawn by the author follow. One was done from imagination, the other from nature. One is extreme in its amount of detail. The other goes to the opposite extreme. We could label them minimal and maximal (in terms of their information content). Which do you believe was purely imaginative?

References

1. Minsky, M. "Steps Toward Artificial Intelligence", Proc. IRE, 8-30, Jan.1961, also in Feigenbaum, E. and Feldman, J. (eds.), Computers and Thought, NY: McGraw-Hill, 1963.
2. Polya, G. Induction and Analogy in Mathematics, Princeton, New Jersey: Princeton University Press, 1954.
3. Steen, L., "The Science of Patterns," Science, pp. 611-616, 29 April 1988, The American Association for the Advancement of Science.
4. Devlin, K., Mathematics: The Science of Patterns, NY: W. H. Freeman and Co., 1994.
5. Muroga, S., Threshold Logic and Its Applications. New York, NY: Wiley, 1971.
6. Lewis, P. and Coates, C., Threshold Logic. New York, NY: Wiley, 1967.

Coins in Two Lines Figure 1. Structure, Dimension, and Quantity	Regular Polygons and Inscribed Circles Figure 2. Shape, Symmetry, and Limit
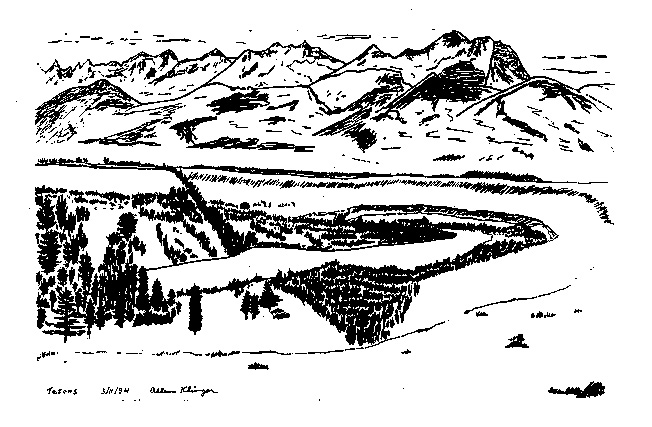
Wyoming Scene with Many Textures Figure 3. Snake River	Limited and Dominated by Line Figure 4. Upper New York Harbor

We don't know whether the first patterns humans communicated to each other were auditory or pictorial. Still the cave paintings in Europe are impressive to us today. What is behind that impressive nature is the power of what we call art. In analyzing patterns, whether in medicine (a practical art) or mathematics (queen of the sciences) one comes up against the question: what is art? Michelangelo's comment may be the last word on that subject: Trifles make perfection, and perfection is no trifle. In comparing the two sets of figures above we could say that Figures 1 and 2 are representations: either a sketch of real coins or a diagram about polygons and circles. Figures 3 and 4 also represent nature but the way they do that might be akin to art.

Sets, Hierarchy and Statistics
The view of patterns as elements of sets reflects the human ability to learn and abstract (focus in on a general property and disregard interfering detail). Humans both discern and develop patterns. Aspects of nature (seasons, star constellations) or quantitative reasoning (even numbers, formulae for perimeter, area and volume) are examples where people perceive the pattern present. The case of writing where there is a means for transmitting letters/numbers or characters to future generations supplies an example of pattern development, through the cases of different styles and fonts. Hofstadter [1] develops the idea of letters' similarities and differences. Obvious variations present no barrier to accurate future recognition. The general understanding of recognition involves some means by which we teach others to see general characteristics in representative samples.

A group of representative samples comprises elements within that pattern's set or class. This idea can be made concrete by imagining continuous variation as defining the pattern. Then the presence of samples, some specific patterns, gives some idea about the set but doesn't fully describe it. To know about the overall set we need a rule for generating objects, or in the case of finite sets all the samples.

Because of the use of randomness to model pattern analysis textbooks often present information diagrammatically. For instance, when choosing random scalar numbers one speaks of them as a sample of elements on the real line. No matter how many pattern instances are available the only thing they represent is a rough approximation to the real set. The pattern set represents all things of that common type. It is an idealization just as is a prototype, template, paradigm or ideal image.

The field of Statistics is explicitly concerned with reasoning based on samples, with decision-making as a central aspect, as in Bayes decision rule. When pattern instances are available in large enough quantities it is reasonable to use an approach based on that field; there are several such approaches. They range from situations using Probability assumptions about causes, to those using only computation based on observed data (Clustering). [Probability is a field within Mathematics. So is Statistics, and its Clustering sub-field, but the applied nature of these two areas differs from the theorem-and-proof basis of Probability.]

Probability is a well-thought of subdiscipline of Mathematics. It involves such clear concepts as dependence, independence, correlation, mean, variance/standard-deviation, and distributions' parameters.

Conditional Probability Notation and Decisions
The word form of a definition of conditional probability is:
Probability (A given B) is same as Probability (A and B) divided by the Probability (B), when the Probability of B is strictly positive. (1)
But the central idea when dealing with conditional relationships has to do with whether it is meaningful or not. When a pair of events have no influence on one another's occurrence we say they are independent.

While the expression in (1) is purely formal it is a good idea to return to the sample space, the list of all possible outcomes. For rolling a six-sided die with dots ranging from one to six shown on each side, there are six outcomes and that is the size of the sample space. For two such items, called rolling the dice, any number of dots on one die can exist with either of the six possibilities on the other, leading to a sample space of size thirty-six. In the case of a normal or Gaussian random scalar, there are infinitely many elements in the sample space since values ranging from minus infinity to plus infinity could occur.

The conditional probability definition yields an expression used in decision-making called Bayes Theorem. In particular it can be the basis of assigning a pattern to one of several possible classes (sets). The following details the derivation of that expression.
From twice applying multiplication to clear the ratios in the definition of conditional probability (1), with denominators strictly positive we obtain the formula (2) :

Probability (A) Probability (B given A) = P(A) P(B| A) = P(B) P(A| B) = Probability (B) Probability (A given B) (2)

The restatement of (2) that follows is Bayes Theorem (an equation, not a theorem):

P(B| A) = P(A| B) P(B) /P(A) (3)

To see how the expression (3) could be used consider the real situation. If we know that the pattern class is a certain case we will call "one" then we could collect a large number of samples of that type. We want to use a summary of that information to decide whether a specific unknown class pattern is of type one (or two, three, etc.). Let the pattern sample data be A, and the class number be B. The collected information about samples from some numbered class B, represents a probability law for varieties of values, given that we began in that class [P(A| B) in (3)]. For decisions one needs to compare the probabilities at the left of equation (3) as B ranges over the classes for a given pattern A. One assigns a particular x (A) to the class B where the probability p(B| A) is largest. (This is called the Bayes decision.) The general pattern notation takes x as an unknown class pattern represented by a vector of features. We can think of the specific set of values of x as event A.

No matter what we know about statistics and decision rules there are many human pattern analysis situations that fall outside that domain. Information about number sequences like that in [2], presence and absence of visually-depicted objects in scenes (Figure 5, [3]), and questions about comparing items that depict pattern relationships (as investigated by Bongard [4]; Figures 6, 7 and 8) all lie outside this model of statistical decisions for pattern recognition.

References

1. Hofstadter, D., "on seeing A's and seeing As," SEHR, 4, issue 2: Constructions of the Mind, Updated July 22, 1995, http://www.stanford.edu/group/SHR/4-2/text/hofstadter.html .
2. Sloane, N., Plouffe, S., The Encyclopedia of Integer Sequences, San Diego CA: Academic Press, 1995.
3. holland herald (KLM airline magazine), July 2002, p. 46, "Spot the eight differences."
4. Bongard, M., Pattern Recognition, New York: Spartan Books, 1970.

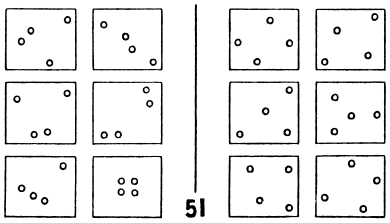
Figure 5. Beach Scene [3]: Eight Differences	Figure 6. Bongard 51 [4]	In 51 the left third row first column and the right second row first column are alike
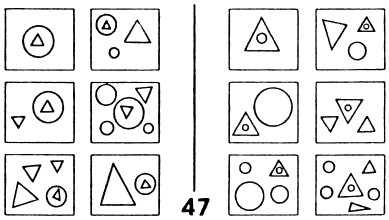
Find the corresponding left-right elements in Figure 7. (Use the images as shown or visit [1] where they appear full size.)	Figure 7. Bongard 47 [4]
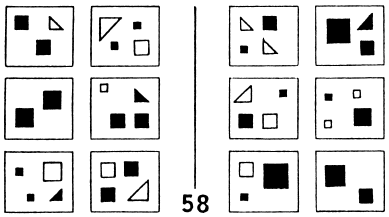
Find the corresponding left-right elements in Figure 8. (Use the images as shown or visit [1] where they appear full size.)	Figure 8. Bongard 58 [4]

---

10/17/02 Version

Pattern_1

www.cs.ucla.edu/~klinger/pami/pattern_1.html