Improving Access to Fundamental Concepts
Allen Klinger
Synopsis
This paper concerns using the ability of inter-net computer communications
software and hardware to connect people to practical problems. Current
technologies support disseminating visual information, sounds, animations, as
well as text files. Pedagogically those methods enable improvements to engage
people in abstract ideas where currently many obtain only an acquaintance with
related symbols.
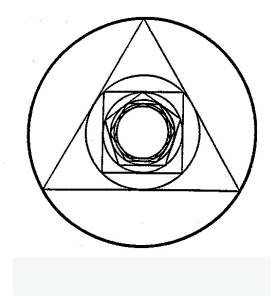
The heart of this article involves three visuals, a lunar image, a three-dimensional solid with hexagonal-equator composed of rectangular and triangular faces, and a series of nested circles with polygons inscribed (the largest polygon is a triangle) with successively higher numbers of edges. All three images can also be seen easily by using an inter-net browser (Netscape Navigator, Internet Explorer, Safari, Mozilla, etc.); their URLs are in the text. The image of circles with inscribed polygons is from a book by Kasner and Newman, first published in 1940; those authors demonstrate there that ancient Greeks knew about limits and accurately evaluated the limit value of inscribed circles’ radii.
The paper concludes with
descriptions of, and pointers to, thought-provoking topics. Each topic is two
things. On one hand each challenges the reader, and requires work. But each
stimulates review of some basic notion. The text suggests some connections to
fundamental concepts and useful tools.
Introduction
Both engineering
students and people in the general community can benefit from accessing
inter-net materials that explain abstract ideas. These materials can be text
files, but also hypertext (links to related topics), images, animations, and
sounds. Because practical problems deal with real situations, visual methods
often lead
to, or motivate solutions.
Visual and animated
material fix ideas in one’s mind; they make concepts memorable. In general visual items make the material more
understandable and hence accessible to more people. The following three examples
are two- and three-dimensional objects with the latter shown through a planar
image generated by computer graphics software (all also can be viewed from
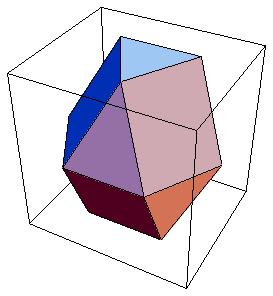
their URLs). One portrays a lunar image. The next is a three-dimensional solid
composed of rectangular and triangular faces (and a hexagon for its equatorial
edges). The last one is a series of nested circles with polygons inscribed (the
largest one is a triangle). The polygons with successively higher numbers of
edges go inside the circles of shrinking radii.

http://www.cs.ucla.edu/~klinger/nmath/2circles_9_13_04.pdf
Figure 1.
Lunar Image Constructed by Circles
http://www.cs.ucla.edu/~klinger/tet1w.gif
Figure 2. Solid Constructed from
Vertices’ Coordinates
http://www.cs.ucla.edu/~klinger/radiia.jpg
Figure 3. Image With Polygons Inscribed
in Circles [1]
Partitions
Three questions each deal differently with physical division. The first is quickly stated in words: “can a circular pizza be divided into eight equal portions with exactly three straight line cuts?” (Many find this difficult.) Addition, subtraction, and partitioning an entity into fractions, are commonly understood, yet can lead to difficulty with: “can you combine the four digits 1, 5, 5, 5, using only the arithmetic operations: plus +, minus -, times x, and divide, possibly using parentheses; to obtain the value 24?” The third is an ancient question. It is “can you divide nine loaves of bread among ten men so that each has a fair share?” [In addition to being equal in quantity the portions should seeming to be the same, as much as possible.] It too asks about applying fundamental knowledge to a practical end.
Answers to all three
also appear at or are reachable from web URLs. The following two figures show
some visual aspects of these questions. [Regarding the second figure,
additional material about the modern
and ancient Egyptian
views of fair division appears at http://www.cs.ucla.edu/~klinger/efractions.html.
People seeking an animated statement of the 24-question, with a clickable
button to reach the solution, may consult http://www.cs.ucla.edu/~klinger/nmath/puzzle1555.html.]
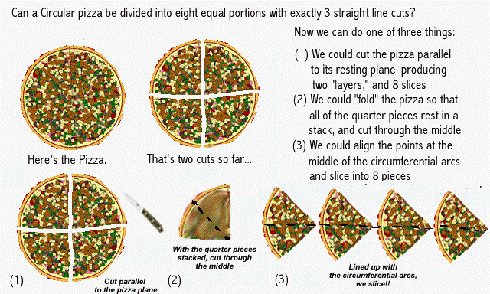
http://www.cs.ucla.edu/~klinger/pizza1.jpg
Figure 4. Pizza Image With Text [2]
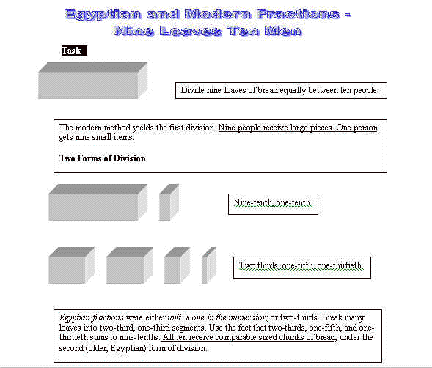
http://www.cs.ucla.edu/~klinger/eimage.jpg
Figure 5. Modern and Ancient Egyptian
Views of Equal
Whether the “24 from 1, 5, 5, 5” question answer
comes easily depends on how comfortable one is with fractions. The irreverent
image in Figure 6 and delays in getting a 24 answer reveal that this is an
uncomfortable subject.
![]()
http://www.cs.ucla.edu/~klinger/19-95c.jpg
Figure 6. Not The Best Way to Cancel
Internet Access to Images
Only an elementary level of skill came into the creation of Figures 1, 3, and 5. Some knowledge of lists and the graphics behind Mathematica images supported Figure 2. Figure 4 was by someone with design and art skills. The URL in Figure 6 leads to an animation. All involve (see acknowledgement) interaction with students, colleagues, and books. While these files demonstrate the power available from using computer graphics and animation along with text, to present material via the inter-net, much more sophisticated still visuals, dynamic, and evolving materials are accessible.
First, consider the
beauty and insight conveyed by the URLs in Table 1. The material there concerns
just two things: a) turning a sphere inside out; and b) sixty-three famous
curves. The first two URLs play movies showing the inside-out transition. The
last URL lets one load programs that enable selection of the parameters of the
curve in question.
On Turning a Sphere Inside Out
http://www.th.physik.uni-bonn.de/th/People/netah/cy/movies/sphere.mpg
http://www.geom.uiuc.edu/docs/outreach/oi/evert.qt
http://www.akpeters.com/product.asp?ProdCode=2183
http://www.xs4all.nl/~alife/sphere1.htm
Links to Parametrically Changeable Versions of Sixty-Three Famous Curves
http://www-gap.dcs.st-and.ac.uk/~history/Curves/Curves.html
Table 1. URLs of Material Available From the Inter-Net
Second, although the Figure 1 image may be familiar from looking at
the night sky, embedding that knowledge about overlapping circles in a source
statement (“familiar from looking at the night sky”), is itself not part of
every course covering geometry. Likewise other practical (or discovery and
origin aspects) aren’t always available. But an embedding of that image with
related materials is now accomplished (although not by someone who interacts
with students in K-12 education) via:
http://www.cs.ucla.edu/~klinger/nmath/ellipse.html
This material connects overlapping circles to
squares and ellipses. It does this both by written text and by pointers (links,
hypertext).
Conclusion
Perhaps you now believe
that the pizza cutting let you see more in 23 = 8 than you had
before. Possibly the fourteen faces in tet1.jpg and tet1w.gif seem a good display of
twelve points equidistant from the origin, six in the equatorial plane, three
at each pole. But almost surely you are now in possession of ways to see
sixty-three famous curves, and watch a sphere turn inside out. All that makes
you a candidate for advertising how the inter-net improves access to
mathematical knowledge.
References
[1] Kasner, Edward and Newman, James R., Mathematics and the
Imagination, NY:
Simon and Schuster, 1940; Redmond: WA, Tempus Books of Microsoft Press, 1989;
pp. 310-312
[2] Gillings, Richard J., Mathematics in the Time of the Pharaohs, Cambridge, MA: The MIT Press,
1972; NY: Dover Publications, Inc., 1982, ISBN 0-486-24315-X.
Acknowledgement
Gavin Wu created the image labeled pizza1.jpg that
appears in Figure 2.
Yu-Chian Tseng created the animation labeled puzzle1555.html .
Walter Karplus called my attention to the
Figure 6 cancellation.
Eskandar Ensafi and unknown Wolfram
Research employees assisted in the creation of tet1.jpg and tet1w.gif. Dorene Lau
created material at dorene/math3.htm that was excerpted for nmath/ellipse.html .