Internet Exposition, Visualization and Assessment

Allen Klinger

6 21 02

This paper describes ways to use today’s technology to foster approaches to Mathematics through inquiry, a means that stresses involvement, motivation, and informality. We show how to create new materials as well as integrate past items composed by authorities. Fundamentally we reflect that the internet supports new kinds of tutorial exposition. Using them effectively means employing technological methods to support follow-up.

A second aspect of an expository style based on inter-net availability is the relative ease of integrating still or animated images, and sounds, into a new tutorial. The connectedness of knowledge is a pragmatic reality due to high computer processing speeds and communication networks. These technologies support visual and auditory information presentation. They in turn foster visualization in reasoning, analysis and design.

Material posted to the internet becomes a democratic force in this sense. Popularly available items are potentially usable for informal education. The third topic involves methods to evaluate what informal and formal learners know about topics, a necessity if information is supplied outside an organizational framework. This means measuring accomplishments. This can be done assigning highest scores to those who honestly disclose what they know.

1. Topics and Technology.

This section describes using software tools and hardware infrastructure to disseminate a personal view of Mathematics. Notation and style are substantial parts of ordinary mathematical exposition. Nevertheless the widespread use of computer network technology leads toward freedom to rethink those aspects. In fact having a sense of modern computer technology may tend one neither toward approved approaches of Mathematics nor those of Computer Science or Engineering. Instead creating inter-net materials can be for one’s own pleasure. In my case I’ve taken a path of presenting knowledge in a form so that others can more readily go forward.

The tradition of teaching difficult concepts through card games, puzzles and riddles is well established. It would be easy to list examples, even books: many volumes are collections of them. But that is an informal manner of Mathematics education. It stands in contrast to tomes on Algebra, Trigonometry, Calculus, etc. Nevertheless the recurrent failure to create positive mathematical interest in vast portions of a general population, one that is oriented toward gambling games, means that there are needs. I assert here that today’s technology gives means to meet those needs. This begins with a program of exposition based on the unique attributes of the inter-net. The attributes depend on such a wide array of diverse technologies that even listing their main academic sources is daunting. They certainly include Computer Science: data structures, networks, theory, programming languages; as well as contemporary computer utilities: Macromedia’s Flash, the markup languages such as HTML, and media players such as Apple QuickTime.

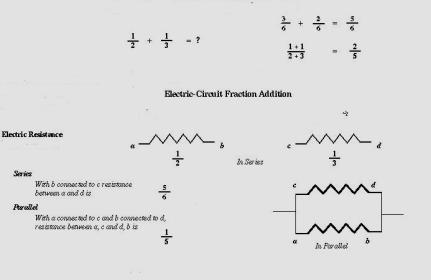
Based on inquiry and an evolving sense of what troubles those individuals who dislike Math, I recommend fractions as one fundamental area to investigate. For many of us our understanding of such a simple subject might make this seem a foolish suggestion. Still connecting current views about the rigid equivalence between ratios and decimal equivalents, to subtleties of thought that arise when one considers how the ancient Egyptians would have divided nine loaves of bread among ten men, might lead to less skepticism. Even that amount surely would decline if the series and parallel forms of addition of two fractional resistors in Electronics/Electrical Engineering, say one of a half Ohm value and the other, a third Ohm, were considered. Finally that same “simple” addition takes on a completely different nature if baseball batting average were to be computed (for a player who bats one hit in three at bats on day one, and one in two at bats day two).

Two simple statements give many (and gave me) difficulties. They both show the thesis of this paper: simple things are deeply connected with Mathematical knowledge. In short form they are:

1. Can one divide a circular pizza pie into eight exactly equal slices with just three straight line cuts?

2. Can you make twenty-four from three five’s, a one, using the four arithmetic operations, plus, minus, times and divide, and grouping by parentheses?

The first is a tricky way of leading into a more advanced concept than is usually part of elementary arithmetic (dividing) or geometry (circles, sectors). But the second points to the relative discomfort most people have with fractions.

2. Writing and Showing.

The inter-net supports branching exposition. The markup language, HTML, is the fundamental enabling technology. To use HTML one needs to become acquainted with some facts from a file easily found with a search engine. Once that point has happened, it is relatively easy to present related technical topics in linked files. A link or pointer (called an anchor in HTML) is a location-finding datum. It supports transition from one file to another. This is particularly important in Mathematics exposition where students have difficulties due to unfamiliarity with related topics. To a new learner Mathematics seems like a simultaneous encounter with a large number of concepts.

Even more interesting, the same technical features that allow branching also support viewing images, hearing sounds, and displaying animations. Both of the above questions have answers that are better shown than written about. An image that displays movements to the answer can be even more powerful. That is true even when it represents a special case, not the general instance, something easily seen by viewing the following images. Figure 1 represents a not-equal-side pentagon. Figure 2 shows six different representations of the number or quantity five. A similar series for the quantities one through five follows in Figure 3.

Figure 1. Five-Sided Shape

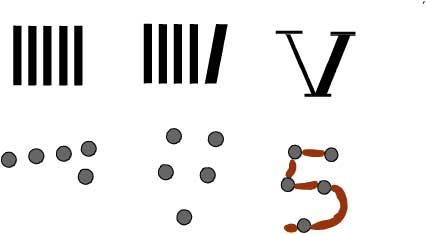
Figure 2. Six Representations of Quantity Five

Figure 3. Three Representations of Tallying the First Five Quantities

Figure 1 could lead into a Geometry lesson. But since it was impossible to generate the fourteen-faced solid entity without Analytical Geometry, List Notation (a Computer Science topic), and the contemporary computer software Mathematica, there are many directions that one can go to from that five-sided shape.

The visionary 1945 paper by Vannevar Bush introduced the notion of knowledge as an interconnected set. The technical notion he innovated in “As We May Think,” is of linkages or simply links from one topic to another. That idea became the essence of computer programming where a link today is also sometimes called a pointer (see e.g., the seminal work by Knuth or the Klinger encyclopedia article listed below). Thought about what interconnected or linked ideas represent is well expressed in the related term, hyperlink or hypertext. There is a worthwhile article that expressed technical realities that now are solidly entrenched through the proliferation of the inter-net. A survey article published in 1987 by Jeff Conklin in an engineering publication, expresses the wonderful reality that is upon us today when we consider inter-net exposition. We will see that there are tools and means for making evident the connections of Mathematical material to History, Culture, Art, Music, and other subjects, without compromising its clarity or quality.

Figure 2 takes Roman numbers as a starting point for understanding the origins of what are commonly called Arabic numerals. This static visual conveys a point made by Hadamard in a lecture. The truly remarkable thing about current software and computer hardware is that they are a technological means for conveying the full notion he presented, through animations. (See Software within References.) Figure 3 uses modern computer software as an enabling technology to display tally marks from three different cultures: Western, Vietnamese, and Chinese. There are many differences between exposition based on the inter-net and associated software technologies and that in books and journals. For instance, the inter-net easily enables displaying a multicultural view of quantitative subjects just as is shown in Figure 3. The Greek culture gave rise to the area of Mathematics, yet few are aware that this knowledge included the concept of limit. But Figure 4 makes it visually apparent that this too was known in the Greek world.

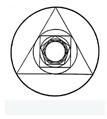
Figure 4. Nested Regular Polygons With Inscribed Circles

3. Visual Organization and Innovation

Although the inter-net began in the West it has great potential for good on a worldwide basis. The cost of books is prohibitive in many countries. That recognition has spawned activities like posting the text of fundamental works to the web (see e.g., Project Gutenberg and related distribution activities for ASCII or .txt format of key books). Although both Figure 4 and another one on limits shown in Kasner & Newman, are now available from the web through http://www.cs.ucla.edu/~klinger, there are many images from other realms found in Ascher’s book, but not yet available. This is not through the fault of technology. Rather it is a matter of organizing students to scan in images there from Polynesian, and African cultures: the technology exists to distribute visual matter in low cost way analogous to the text distribution activities.

But a wealth of material is already on the web. For example:

“Stanislaw Ulam … studied at the Lwów Polytechnic Institute, in the Department of General Studies (the quota had been reached in the Department of Electrical Engineering) beginning … 1927. In 1933, (he) was conferred the first Doctoral degree from the Department of General Studies at the Polytechnic Institute.” (Image and text appear courtesy of Corin Anderson, initially from the web site http://www.the4cs.com/~corin/motm/stan_ulam.html; for Ulam’s relationship to the history of the hydrogen or fusion bomb also see the appended excerpt from http://www.pbs.org/wgbh/amex/bomb/peopleevents/pandeAMEX74.html) Both this web reference and the book by Solomon Golomb present examples where visual thinking by Electrical Engineers led to Mathematical innovation. The role visualization plays is one theme of James Adams, in his book. His work began with a Mechanical Engineering design course at Stanford University. [The nine-dot four-line problem he presents in the book generated the phrase “think outside the box.”]

Richard Feynmann’s physical inventions (Feynmann diagrams) go along with remarkable visualization ability. Some images he drew are presented in the “Surely You’re Joking Mr. Feynman” book

Ulam and Golomb contributed solutions to real world problems. Ulam visualized a means to promote nuclear fusion. Golomb produced the means for image transmission from space vehicles. The visual elements in his book are related to a secure code for overcoming the effects of random noise. Both Ulam and Golomb used visual reasoning. What inter-net exposition can do is to place the average individual in front of problems that have the effect of requiring some form of visual analysis.

Some would protest that this is “too complicated,” or that “problems form the widespread aversion to Mathematics,” The immediate counter to that is the popularity of gambling: Las Vegas, government-sponsored lotteries, and casino activities. Games with cards, boards, and other formats, are seen as entertainments, not drudgery. Architects ranging from Escher to others known more from their residential or public building designs, or their theoretical contributions as in the case of Christopher Alexander, are of widespread interest and their designs (see Schindler’s house number in Figure 5.), images, and books sought after.

Figure 5. 20^th Century Architect Schindler’s House Number Design for “175 Greenfield”

Both architects and engineers work in the real world: they apply knowledge to make things.

The two fields value models if useable/useful, but are ready to discard them when they are seen to be unhelpful. Figure 5 discards the notion of isolated characters for numbers: it is more useful to hang a single metallic sign based on small segments joining the offset two horizontal bars. The same process is clearly involved when calculating the addition of two fractions, either in sports statistics [“total successes” divided by “total trials”] or the familiar to Electrical Engineers formula for the parallel combination of two resistances (see appendix). When considering the three numerical results for fraction addition shown in Figure 6. one must consider the usefulness of discarding the ordinary method taught in most elementary schools.

Figure 6. Fraction Addition – Sports and Electric Resistance Alternatives

Figure 7. Spatial Relationship - Thirteen Equidistant Points on Three Planes

4. Assessing Learning Accomplished

For more than sixty years there has been a remarkably successful methodology for determining exactly what individuals know. The triangle in the following figure, and associated numerical weights derived and presented in the FIE paper show one version of that approach. Here there is a visual presentation of thirteen responses to three alternative completions of a statement. The non-vertex points represent partial knowledge. The triangle mid-point signifies “nothing known”. [Emir Shuford. has posted to the web many papers concerning this technology. James Bruno first communicated to me three things that formed part of that paper. These are: using discrete points, an alphabetic labeling, and the relative weights or value of answers at all thirteen of the triangle points.]

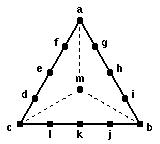
Figure 7. Thirteen Responses to Three Statement Completions

5. Opportunities

Today very powerful computer software tools exist that implement mathematical notation, knowledge, and procedures (APL, Mathematica, Maple, etc.). Notwithstanding their availability, the tendency is for there to be fewer individuals seeking out Mathematics as a source of basic knowledge. Beginning with a traditional educational infrastructure to disseminate a personal view of Mathematics. Notation and others can more readily go forward. In spite of the existence of listserve, newsgroup, and electronic mail dissemination of Mathematics, today in the United States Computer Science graduating seniors are hesitant to express fundamental notions in their field to their peers. They avoid showing interest in coding, modulo, computational issues.

The fundamentals of the world dynamic are that most economic opportunity goes to those who have information, or at minimum, can work effectively with it.

6. Appendix

Thermonuclear Weapon [Source: PBS in References]

President Truman announced in January 1950 that the United States was about to embark on an all-out effort to develop a hydrogen bomb, Ulam began calculating whether physicist Edward Teller's design … would work. He comments: "We filled page upon page with calculations... I do not know how many man hours were spent ..."

Ultimately, Ulam and a fellow mathematician Cornelius Everett concluded that Teller's model … would never work. ... But a year later Ulam accidentally came up with a new scheme that would prove to be a breakthrough, and he reluctantly took it to Teller. Teller recognized that, though there were problems with the idea, Ulam had hit on the solution. Together the two men converted it into a design for the superbomb that everyone at Los Alamos immediately recognized would work.

Their plan was to place an atom bomb inside a heavy shell that would also contain a capsule of hydrogen fuel. When the atom bomb exploded, in the fraction of a second before the whole assembly blew itself apart, the shell would confine the radiation from the atomic blast long enough to heat and compress the hydrogen fuel, setting off a fusion reaction. Central to Ulam's idea was the use of material surrounding the fuel capsule that would magnify the energy of the radiation.

Decades later physicist Hans Bethe wrote: "The new concept was to me, who had been rather closely associated with the program, about as surprising as the discovery of fission had been to physicists in 1939 …”

Electric Resistance

Ohm’s Law: E = I * R (1) E (Volts) = I (Amperes) * R (Ohms)

Series - R = R₁ + R₂

Parallel - Apply (1) noting that the same electric potential E goes across the total resistance R and also each of the two parts, R₁ and R₂. Since the current I divides it equals the sum I₁ + I₂. That means:

E = I * R = (I₁ + I₂) * R = I₁ * R₁ (2)

E = I * R = (I₁ + I₂) * R = I₂ * R₂ (3)

The remainder involves algebraic manipulation of the rightmost equalities of (2) and (3). This process is aided by substituting I for (I₁ + I₂), Replacing I₂ by (I - I₁) is helpful. The solution of the two equations for R or 1/R respectively yields:

R = 1/[(1/ R₁) + (1/ R₂)] (4)

1/R = (1/ R₁) + (1/ R₂) (5)

The following steps lead to these results.

(2) -> R = [I₁ * R₁]/[ I₁ + I₂] (2’)

(3) -> R = [I₂ * R₂]/[ I₁ + I₂] = [(I - I₁)/I] * R₂ (3’)

Substituting (2’) in (3’) and solution of the result for R yields (4) and (5).

Multiplying (4) by R₁* R₂ yields the parallel resistance formula:

R = [R₁ * R₂]/[ R₁ + R₂]/

References

Bush, Vannevar, “As We May Think,” The Atlantic Monthly, Vol. 176, No. 1 (July, 1945), 101-108. Available from http://www.theatlantic.com/unbound/flashbks/computer/bushf.htm

Conklin, Jeff, “Hypertext: An Introduction and Survey,” IEEE Computer, Vol. 20, No. 9 (1987), 17-41.

Golomb, Solomon W., Polyominoes [with more than 190 diagrams by Warren Lushbaugh, NY: Charles Scribner's Sons, 1965], Second Edition, Princeton NJ: Princeton Univ. Press, 1994.

Ulam, S. M., Adventures of a Mathematician, Berkeley CA: Univ. of Calif. Press, 1991.

Klinger, Allen, Human Computer Interactive Systems, NY: Plenum Press

Alexander, Christopher

Klinger, Allen and Salingaros, Nikitas

Klinger, Allen, “Training and Thinking,”

Klinger, Allen, “Experimental Validation of Learning Accomplishment,” Proc. Frontiers in Education, 1997.

Klinger, Allen, Finelli, Cynthia J. and Budny, Dan D., “Improving the Classroom Environment,” Proc. Frontiers in Education, San Juan, Puerto Rico, 1999.

Finelli, Cynthia J., Klinger, Allen, and Budney, Dan D., “Strategies for Improving the Classroom Environment,” ASEE Journal of Engineering Education (invited), Oct. 2001, 90, 4, 491-498.

Software

Macromedia, Dreamweaver (web files), Flash (animations).

Adobe, Photoshop (image-handling), Illustrator(drawing).

Web Files

Concerning Stanislaw Ulam

Corin Anderson http://www.the4cs.com/~corin/motm/stan_ulam.html

Public Broadcasting System (PBS)

http://www.pbs.org/wgbh/amex/bomb/peopleevents/pandeAMEX74.html