The Genesys System:
Evolution as a Theme in Artificial Life
David Jefferson, Robert Collins, Claus Cooper
Michael Dyer, Margot Flowers, Richard Korf
Charles Taylor, Alan Wang
UCLA
Los Angeles, California 90024
1. Introduction
This paper describes the Genesys system, built by the UCLA Artificial Life group in a study to test the feasibility of using evolution to design programs with complex behavior. Genesys takes a population of programs encoded as bit strings, and evolves them by genetic algorithm (Holland 1975) to optimize their behavior on some specific task. This work was motivated by the following questions:
Can evolution be used to create programs, i.e. can the text of a program, rather than parameters to a program, be the genetic material in a genetic algorithm?
If so, at what pupulation size, and with what mutation rate, recombination rate, selection parameters and mating strategy? Is it computationally feasible to evolve programs represented as strings hundreds of bits long?
What representations for programs are appropriate for genetic algorithms? In particular, are recurrent artificial neural nets suitable for design by genetic algorithm?
Can outstanding biological problems in the theory of evolution be attacked by genetic algorithms over populations of artificial animals?
This paper is a report on preliminary work directed toward these questions, some of which have now been resolved to our satisfaction.
The evolutionary exercise we describe here was inspired by the behavior of ants. Certain kinds of ants lay down odor trails between their nest and a food site to aid in the process of collective foraging (Holldobler and Wilson 1990). The trails are crooked and "noisy", and fade with time as the pheromone chemicals disperse. This trail-following ability is quite remarkable, and clearly required the evolution of elaborate nervous system structures (present in modern ants but not in the ancestral population).
We designed a highly simplified task called tracker that superficially resembles ant trail-following, in order to see if we could evolve artificial ants with complex behavior. The tracker task requires the ant to follow a crooked, broken trail of black squares in a white toroidal grid. The trail is not simple, but has a series of turns, gaps, and jumps that are more difficult as the trail progresses. The initial population of animals is constructed by a random process, so that while they have the ability to sense the environment and move around in it, they clearly have no built-in ability to follow trails. However after 100 to 200 generations of evolution by genetic algorithm (depending on other parameters) a large fraction of the population is nearly perfect at the task.
The Genesys system executes a genetic algorithm over either of two distinct representations for programs: (a) finite state automata (FSAs), or (b) artificial neural nets (ANNs). It runs on a 16K-processor Connection Machine (CM2) with 8K bytes of memory per processor (Hillis 1987). We typically run with a population of 64K organisms, and execution takes less than 30 seconds per generation.
The original reason for working with two representations was our inability to decide, on any fundamental grounds, which was the better computational model for this task, and which was the better representation for studying evolution of behavior (a distinctly different question). It turned out that after going to some length to make the two representations as comparable as possible, the FSA representation consistently performed slightly better than the ANN representation on the tracker task. However, we have not come to a full understanding of why this was so, and we do not necessarily believe the result generalizes in any meaningful way to other tasks or to larger organisms than the ones we were working with. Rather than decide which of the two representations was "better" for the study, we concluded that, regardless of the answer, working with two representations was extremely important for completely different methodological reasons. First, it tends to eliminate the potential problem that an evolutionary phenomenon we observe might be an artifact of the representation and not a genuine feature of evolution. Second, it focuses attention on a fundamental issue that all similar studies must face in the future: just what is a good computational representation of living organisms? We expect that this representational issue will be of fundamental importance in future artificial life studies.
Another issue we are interested in is the design of neural nets. In this paper we demonstrate that genetic algorithms can be used as an alternative to learning mechanisms for modifying the weights in recurrent artificial neural nets (ANNs) to improve their performance at a particular task (Montana and Davis 1989), (Goldberg 1989), (Goldberg and Holland 1988). We believe there are several major advantages to using genetic algorithms (in addition to learning) for the design of ANNs. First, the kind of performance feedback needed to drive the weight change procedure is simple. Although there is a need for some measure of the performance of an ANN on the task, there is no need to be able to measure the difference between its performance and the ideal performance, as is required by e.g. back propagation (Rumelhart and McClelland 1986). Second, our evolutionary mechanism applies without change to both recurrent and nonrecurrent nets alike (Pearlmutter 1989) (Ellman 1988). Third, a genetic algorithm can take advantage of massively parallel trials at the task (by a whole population at once), whereas learning protocols inherently require sequential trials (by a single individual).
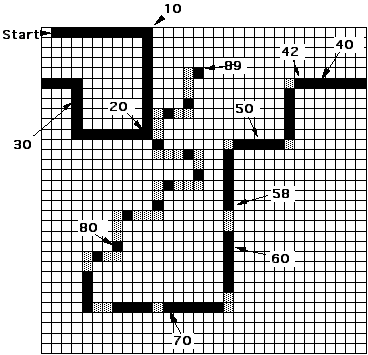
2. The Tracker Task
Our experiments were conducted using the following task. An "ant" is placed in a two-dimensional toroidal grid at the beginning of a broken rectilinear trail as shown in Figure 1. This trail, called the John Muir Trail, is used throughout this paper. The ant’s task is to move from square to square, traversing as much of the trail as possible in 200 time steps. The ant is considered to erase the trail to prevent backtracking as it moves, and its success is measured by the number of trail squares it traverses. It is free to wander off the trail and pick it up elsewhere, but that is not an efficient strategy.

Figure 1: The John Muir trail in 32 x 32 toroidal grid. Scores for reaching various landmarks are indicated. (Gray squares are not part of the trail; they are visual aids to the reader.)
An ant always stands in one cell, facing one of the cardinal directions (N, S, E, W), and can "see" only the cell ahead of it (Figure 2). It thus receives one bit of input per unit time about where the trail is. At each time step the ant must make take one of four actions:
a) move forward one step;
b) turn right (without moving);
c) turn left (without moving); or
d) do nothing.
The trail winds around the environment, presenting ever harder challenges. First it includes three right turns followed by a left turn. After a while, starting at trail step 42, it takes several turns where the corner square is missing from the trail. At step 58 there is a double straightaway gap, and then the trail gets progressively more difficult, ending with a series of disconnected knight’s moves and long knight’s moves. The maximum possible score is 89, since that is the number of trail cells.
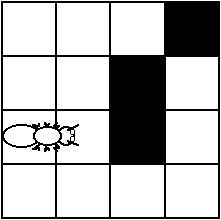
Figure 2: An ant stands in one square and sees only the square ahead of it.
In order for an ant to traverse the trail it must embody an algorithm that causes it to move forward when it sees trail on the square ahead, and to search locally for the continuation of the trail when it does not. It is important to understand that the tracker task does not require general trail following ability; it only requires the ants to traverse this particular trail, starting from the NW corner facing East. Hence we should not be surprised to see the evolution of ants with features adapted to the quirks of this particular trail.
3. The FSA Architecture
Figure 3 shows an example of a finite state automaton that can perform the tracker task. The circles represent states, and the arcs represent transitions the ant undergoes as a function of its current state and its sensory input, each of which takes one time step of the 200 allowed. An arc is labelled with a pair of the form s/a, where s is a 1-bit sensory input indicating whether the ant "sees" a trail square (1) or a nontrail square (0); a indicates which of four actions should be taken: move forward (M), turn left without moving (L), turn right without moving (R), and do nothing (N). The actual FSAs employed in Genesys have up to 32 states.
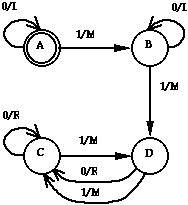
Figure 3: The state transition diagram for a 4-state FSA that achieves a score of 42 on the tracker task.
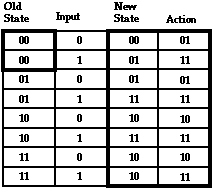
In order to be constructed by a genetic algorithm the FSA must be encoded into a chromosome-like string of bits. The encoding used in Genesys is shown in Figure 4, where the FSA of Figure 3 is arrayed in a table in which each state, input, and move has an arbitrarily-assigned binary value. To uniquely define the FSA, it suffices to indicate the initial state (state A in this example, coded as 00 in binary), and to enumerate in canonical order the New State and Move columns of the State Transition Table (STT). The genome that encodes the FSA in Figure 3 is shown at the bottom of Figure 4. It is the concatenation of initial state and, in canonical order, the last two columns of the STT. Since actual Genesys FSAs have up to 32 states (requiring 5 bits), there are 64 lines in each STT, for a total of 64*(5+2)+5 = 453 bits per genome. Many other encodings for the STT into a string could have been used; this is the only one we have tried, and we have no reason to believe it matters very much.
![]()
Figure 4: The binary-coded State Transition Table (STT) for the FSA in Figure 3. The bit string at the bottom is the genome that encodes this organism.
Actual FSAs that arise during evolution are likely, of course, to have fewer than 32 states, since there is no guarantee that all 32 distinct 5-bit state codes are present in the genome string. As a result, some of the rows in the table for a particular FSA may correspond to states the FSA can never enter and represent "unreachable code". An FSA may have even fewer reachable states if we consider only those used while traversing the John Muir Trail.
4. The ANN architecture
To represent an ant using an artificial neural net ANN we chose a particular recurrent PDP architecture with standard sum-and-threshhold logic in the connection topology shown in Figure 5. There are two input units with an activation of 1 or 0 according to whether the cell ahead of the ant is on the trail or not. One is activated when there is trail, and the other is activated when there is not. (This choice is historical; one input unit could have sufficed.)
Each input unit is connected to each of 5 hidden units and to each of 4 output units. The hidden units are fully connected among themselves, and also to each of the 4 output units. In each time step the net receives input from its sensor units, and the activation signals propagate once along every connection in the network. The ant’s next action is determined by which of the output units has the highest activation (with an arbitrary rule for breaking ties). All of the units have Boolean activations except the output units. Because this is a recurrent net with 5 Boolean hidden units, it can behave as though it has up to 5 bits of memory about its past history on the trail. Each ANN is completely deterministic; it does no learning in its lifetime.
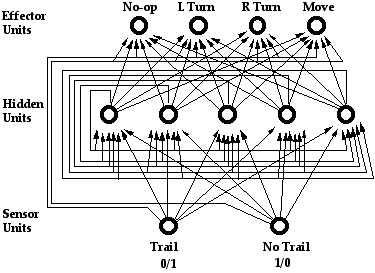
Figure 5: Architecture of the recurrent ANN representing an ant.
To specify an ANN for the trail-following task we must decide on the values of 63 weights, 5 thresholds, and 5 initial activations. In our model the activations of the hidden units are 7 bits each; the weights are 6 bits (ones-complement), and the thresholds are 7 bits each (the high order bits of a 9-bit ones-complement number). The genome representing an ANN-ant is simply the concatenation of all of the weights, thresholds, and initial activations, which takes 63*6 +5*7 + 5*7 = 448 bits. The concatenation is done in a fixed order that was standardized early in the project. Although there are undoubtedly linkage effects in the particular canonical order we chose, we have not explored the consequences of other orders.
5. Comparison of FSA and ANN representations
We have tried to assure that the FSA and ANN representations of ants are as similar as possible in order to make comparisons meaningful. First, we have made the two representations approximately equally powerful computationally. An FSA can have up to 32 states, and hence the equivalent of up to 5 bits of memory. Likewise, since an ANN has 5 recurrent hidden units, each of which passes on 1 bit of information, it can has the equivalent of nearly 5 bits of memory as well. Both representations are fully deterministic. An ant’s "algorithm" is fixed from birth, so apart from the fact that it can gather a few bits of information about the trail, nothing resembling "learning" takes place during an ant’s lifetime.
Because the ANN’s are deterministic, with no more than 5 bits of memory, each of them is behaviorally isomorphic to one of the 32-state FSA organisms. (This fact was very useful in our study since, once we created a tool to translate an ANN to an equivalent FSA, all of our other tools for manipulating FSAs, e.g. for animation or state minimization, applied equally well to ANNs.) However, the reverse is not true; not every FSA can be translated into one of our ANNs because there is a great deal of redundancy in the ANN encoding, and in particular, it is biased so that FSA-ants with the larger numbers of states are underrepresented among the ANN-ants. Hence, we must conclude that our ANN-ants, as a class, are somewhat narrower and less powerful computationally than our FSA-ants (though this is difficult to quantify). There must exist tasks, defined by a trail and time limit, that can be accomplished by some FSA-ant, but not by any ANN-ant.
It is not clear to us whether the fact that there are more behaviorally distinct FSAs than ANNs is an advantage for FSA evolution or a disadvantage. On the one hand, there are many more algorithms using a large number of states that can accomplish the tracker task than there are with a small number of states, so if a large number of states is necessary, that gives the advantage to FSAs. On the other hand, ANNs, by confining evolution to search among the "simpler" algorithms, may avoid getting lost in the huge space of high state-count algorithms.
Besides having the same upper limit in memory capacity, the two representations have approximately the same genome length, i.e. 448 bits for the ANNs and 453 bits for the FSAs. This is important because, all other things being equal, we would expect evolution to take longer on a longer genome than a shorter one because the space being searched by the genetic algorithm grows exponentially with genome length.
6. How difficult is the tracker task, and how difficult is it to design an ant for the tracker task?
The tracker task was carefully designed so that the hand-designed 5-state automaton shown in Figure 6 can traverse the entire trail, although it requires 314 time steps. It only gets a score of 81 in the 200 time steps allowed. The strategy used by this FSA is to move forward whenever it sees a square of trail; when it comes to a point where it does not see the trail in the next square ahead, it turns right (without moving) and checks for trail there. If it finds trail, it moves ahead and continues, but if not, it turns right again. The FSA will turn right a total of 4 times looking trail. After that, it is facing the original direction, and will move forward anyway, even though there is no trail, and will again be prepared to search in all 4 directions again.
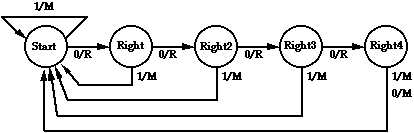
Figure 6: Five state FSA that can traverse the trail in 314 steps, and gets a score of 81 in 200 time steps.
Through evolution we were able to find an FSA with 13 states (the equivalent of less than 4 bits of memory) that can get a perfect score of 89 in 200 time steps (see Figure 8). Hence, we can say that the tracker task itself is not profoundly difficult, since it can be accomplished by a modest-sized FSA.
But just how difficult is the task of designing or discovering an organism that is required to achieve a particular score? That is a completely different issue. Since the tracker task is irregular, it does not yield much to analysis. There is no linearity property, for example, to suggest that it is somehow twice as "difficult" to get a score of 80 as a score of 40. Presumably a skilled human could design an 89-scoring FSA for the tracker task in an hour or two, and an ANN in somewhat more time, but that is not much of a handle on the difficulty of the design task.
To attempt a quantitative calibration of the design difficulty we decided to sample the space of all genomes to discover what fraction of them coded for organisms that got each score. We chose a random sample of over 1.3x109 organisms, of both the FSA and ANN type, and scored each one on the tracker task to produce the results in Table 1. The first column shows the score achieved by the animals in the sample. Columns 2-4 show the sample of FSAs. Column 2 shows the exact number of FSAs from the sample that achieved a particular score; column 2 shows what fraction that represents of the total sample; and column 3 shows the 1 minus the cumulative fraction, i.e. what fraction achieved more than that score. Columns 5-7 are similar to 2-4, but refer to the ANN representation. The sample was chosen by creating random bit strings of the appropriate length (roughly 450 bits each), translating each string into the appropriate organism, and then running the organism on the tracker task as usual to tally its score. Since there are 2450 > 10134 possible genomes, our sample is an inconceivably small fraction of the total, but is still large enough to reliably sample all but the high end of the distributions.
A glance at the table reveals a number of interesting features. For example, 41% of all FSAs, and 68% of all ANNs receive a score of exactly zero! 90% of both FSAs and ANNs get a score of 10 or less, meaning they cannot make it past the first right turn in the trail. (Of course a small positive score can also be achieved by striking off in an odd direction and "accidentally" touching a few squares of trail.) From Figure 1 we note that a score of more than 32 indicates the ability to make the first left turn; a score of more than 42 shows that the animal can get past the first left turn where the corner square is missing, and a score of more than 58 shows it can get past the first straightaway double gap. About 1 in 100,000 FSAs can get past 58, while about 1 in 3,000,000 ANNs can do so. Hence, in a sample of of size 65,536 (the initial generation in most of our evolutionary experiments) there is more than a 55% probability (=1 - (1 - 1.23x10-5)65536) of encountering at least one FSA that can traverse the trail past the double gap, while there is only a 2% probability (=1 - (1 - 3.16x10-7)65536) that there will be such an organism in the initial generation of an ANN run.
The highest FSA score discovered in our sample was 81, of which there were 10 instances; and the highest score found among ANNs was 82, of which there was only one. We can only presume that the higher-scoring organisms are much rarer still, though there is no feasible way to estimate their frequency by sampling. Notice that in our entire sample we never found an FSA that scored higher than the simple one in Figure 6. That exact FSA needs only 5 lines of STT, and can be encoded in 37 bits. Since there are 24 permutations of the 4 non-start states that yield isomorphic FSAs, and since there are just as many FSAs that are isomorphic, but with left turns instead of right turns, the probability of drawing an FSA isomorphic to this one is at least 1 out of 237/(24*2) = 2.86x109. In our sample of 1.3x109, the probability of finding one of these is roughly 36%. And, of course, there are probably other FSAs with similar frequency that are not exactly isomorphic but that still score 81. Later in Section 8, when the results of the evolution over 100 generations is presented, we should note that we typically evolve an 81-scoring FSA within 20 generations with a population of 65536, i.e. after having generated around 106 ants.
We have come to view the tracker task as being not very difficult up to score 81. However, beyond the score of 81 the design task becomes considerably more difficult, not because the John Muir Trail is difficult to traverse per se, but because it is difficult to do so in 200 time steps. It usually takes over 1/3 of the 200 time steps to traverse the last 8 steps of the trail. Hence, we should expect evolution to proceed in such a way that at the beginning there is competition to evolve logic that is basically competent on the trail; in later generations the competition should be for refinements that take advantage of particular features of the trail to save time (steps).
Score Number Fraction 1-Cum. Number Fraction 1-Cum.
of FSAs of FSAs Fraction of ANNs of ANNs Fraction
|
0 |
557258091 |
4.13e-01 |
5.87e-01 |
932924367 |
6.83e-01 |
3.17e-01 |
|
1 |
283207491 |
2.10e-01 |
3.77e-01 |
122460544 |
8.96e-02 |
2.28e-01 |
|
2 |
132410979 |
9.81e-02 |
2.79e-01 |
6275613 |
4.59e-03 |
2.23e-01 |
|
3 |
63272402 |
4.69e-02 |
2.32e-01 |
944545 |
6.91e-04 |
2.23e-01 |
|
4 |
31819298 |
2.36e-02 |
2.09e-01 |
152981 |
1.12e-04 |
2.22e-01 |
|
5 |
18120801 |
1.34e-02 |
1.95e-01 |
345287 |
2.53e-04 |
2.22e-01 |
|
6 |
12985610 |
9.62e-03 |
1.86e-01 |
20361 |
1.49e-05 |
2.22e-01 |
|
7 |
10063926 |
7.46e-03 |
1.78e-01 |
357592 |
2.62e-04 |
2.22e-01 |
|
8 |
9603340 |
7.12e-03 |
1.71e-01 |
379791 |
2.78e-04 |
2.22e-01 |
|
9 |
8472800 |
6.28e-03 |
1.65e-01 |
38531 |
2.82e-05 |
2.22e-01 |
|
10 |
97907623 |
7.26e-02 |
9.22e-02 |
202234068 |
1.48e-01 |
7.37e-02 |
|
11 |
20571404 |
1.52e-02 |
7.69e-02 |
473469 |
3.46e-04 |
7.33e-02 |
|
12 |
9917884 |
7.35e-03 |
6.96e-02 |
141625 |
1.04e-04 |
7.32e-02 |
|
13 |
6084789 |
4.51e-03 |
6.51e-02 |
87343 |
6.39e-05 |
7.31e-02 |
|
14 |
4700955 |
3.48e-03 |
6.16e-02 |
19733 |
1.44e-05 |
7.31e-02 |
|
15 |
3694985 |
2.74e-03 |
5.89e-02 |
30965 |
2.27e-05 |
7.31e-02 |
|
16 |
3392771 |
2.51e-03 |
5.63e-02 |
51634 |
3.78e-05 |
7.31e-02 |
|
17 |
3091910 |
2.29e-03 |
5.40e-02 |
41325 |
3.02e-05 |
7.30e-02 |
|
18 |
3164998 |
2.35e-03 |
5.17e-02 |
244682 |
1.79e-04 |
7.29e-02 |
|
19 |
3665297 |
2.72e-03 |
4.90e-02 |
288731 |
2.11e-04 |
7.27e-02 |
|
20 |
6877796 |
5.10e-03 |
4.39e-02 |
406799 |
2.98e-04 |
7.24e-02 |
|
21 |
8973385 |
6.65e-03 |
3.72e-02 |
1037193 |
7.59e-04 |
7.16e-02 |
|
22 |
2800666 |
2.08e-03 |
3.52e-02 |
83251 |
6.09e-05 |
7.15e-02 |
|
23 |
1831525 |
1.36e-03 |
3.38e-02 |
30711 |
2.25e-05 |
7.15e-02 |
|
24 |
1672638 |
1.24e-03 |
3.26e-02 |
25852 |
1.89e-05 |
7.15e-02 |
|
25 |
1399715 |
1.04e-03 |
3.15e-02 |
74404 |
5.44e-05 |
7.14e-02 |
|
26 |
1466050 |
1.09e-03 |
3.04e-02 |
110140 |
8.06e-05 |
7.14e-02 |
|
27 |
4830484 |
3.58e-03 |
2.69e-02 |
1326186 |
9.70e-04 |
7.04e-02 |
|
28 |
1691564 |
1.25e-03 |
2.56e-02 |
63830 |
4.67e-05 |
7.03e-02 |
|
29 |
1339940 |
9.93e-04 |
2.46e-02 |
101156 |
7.40e-05 |
7.03e-02 |
|
30 |
1087674 |
8.06e-04 |
2.38e-02 |
69337 |
5.07e-05 |
7.02e-02 |
|
31 |
1047454 |
7.76e-04 |
2.30e-02 |
54569 |
3.99e-05 |
7.02e-02 |
|
32 |
9751593 |
7.23e-03 |
1.58e-02 |
1222562 |
8.94e-04 |
6.93e-02 |
|
33 |
1971378 |
1.46e-03 |
1.44e-02 |
30225 |
2.21e-05 |
6.93e-02 |
|
34 |
1104609 |
8.19e-04 |
1.35e-02 |
46131 |
3.38e-05 |
6.92e-02 |
|
35 |
807494 |
5.98e-04 |
1.29e-02 |
70697 |
5.17e-05 |
6.92e-02 |
|
36 |
680257 |
5.04e-04 |
1.24e-02 |
23841 |
1.74e-05 |
6.92e-02 |
|
37 |
614186 |
4.55e-04 |
1.20e-02 |
151106 |
1.11e-04 |
6.90e-02 |
|
38 |
624746 |
4.63e-04 |
1.15e-02 |
28556 |
2.09e-05 |
6.90e-02 |
|
39 |
509548 |
3.78e-04 |
1.11e-02 |
78515 |
5.74e-05 |
6.90e-02 |
|
40 |
522627 |
3.87e-04 |
1.07e-02 |
119459 |
8.74e-05 |
6.89e-02 |
|
41 |
500301 |
3.71e-04 |
1.04e-02 |
896204 |
6.56e-04 |
6.82e-02 |
|
42 |
12110275 |
8.97e-03 |
1.40e-03 |
93179890 |
6.82e-02 |
5.49e-05 |
|
43 |
369162 |
2.74e-04 |
1.13e-03 |
7127 |
5.21e-06 |
4.97e-05 |
|
44 |
170037 |
1.26e-04 |
1.00e-03 |
22279 |
1.63e-05 |
3.34e-05 |
|
45 |
110622 |
8.20e-05 |
9.22e-04 |
2436 |
1.78e-06 |
3.16e-05 |
|
46 |
117108 |
8.68e-05 |
8.35e-04 |
1523 |
1.11e-06 |
3.05e-05 |
|
47 |
638272 |
4.73e-04 |
3.62e-04 |
23420 |
1.71e-05 |
1.33e-05 |
|
48 |
92670 |
6.87e-05 |
2.94e-04 |
1420 |
1.04e-06 |
1.23e-05 |
|
49 |
34361 |
2.55e-05 |
2.68e-04 |
443 |
3.24e-07 |
1.20e-05 |
|
50 |
24808 |
1.84e-05 |
2.50e-04 |
653 |
4.78e-07 |
1.15e-05 |
|
51 |
23300 |
1.73e-05 |
2.32e-04 |
397 |
2.90e-07 |
1.12e-05 |
|
52 |
105961 |
7.85e-05 |
1.54e-04 |
2563 |
1.88e-06 |
9.33e-06 |
|
53 |
24029 |
1.78e-05 |
1.36e-04 |
464 |
3.39e-07 |
8.99e-06 |
|
54 |
12380 |
9.17e-06 |
1.27e-04 |
615 |
4.50e-07 |
8.54e-06 |
|
55 |
9505 |
7.04e-06 |
1.20e-04 |
365 |
2.67e-07 |
8.27e-06 |
|
56 |
9684 |
7.18e-06 |
1.13e-04 |
288 |
2.11e-07 |
8.06e-06 |
|
57 |
10218 |
7.57e-06 |
1.05e-04 |
6715 |
4.91e-06 |
3.15e-06 |
|
58 |
125296 |
9.28e-05 |
1.23e-05 |
3875 |
2.84e-06 |
3.16e-07 |
|
59 |
5488 |
4.07e-06 |
8.26e-06 |
249 |
1.82e-07 |
1.34e-07 |
|
60 |
842 |
6.24e-07 |
7.64e-06 |
2 |
1.46e-09 |
1.32e-07 |
|
61 |
646 |
4.79e-07 |
7.16e-06 |
1 |
7.32e-10 |
1.32e-07 |
|
62 |
641 |
4.75e-07 |
6.69e-06 |
10 |
7.32e-09 |
1.24e-07 |
|
63 |
690 |
5.11e-07 |
6.17e-06 |
6 |
4.39e-09 |
1.20e-07 |
|
64 |
4066 |
3.01e-06 |
3.16e-06 |
32 |
2.34e-08 |
9.66e-08 |
|
65 |
524 |
3.88e-07 |
2.77e-06 |
3 |
2.19e-09 |
9.44e-08 |
|
66 |
230 |
1.70e-07 |
2.60e-06 |
7 |
5.12e-09 |
8.93e-08 |
|
67 |
202 |
1.50e-07 |
2.45e-06 |
3 |
2.19e-09 |
8.71e-08 |
|
68 |
156 |
1.16e-07 |
2.34e-06 |
2 |
1.46e-09 |
8.56e-08 |
|
69 |
183 |
1.36e-07 |
2.20e-06 |
1 |
7.32e-10 |
8.49e-08 |
|
70 |
872 |
6.46e-07 |
1.56e-06 |
10 |
7.32e-09 |
7.76e-08 |
|
71 |
157 |
1.16e-07 |
1.44e-06 |
1 |
7.32e-10 |
7.68e-08 |
|
72 |
117 |
8.67e-08 |
1.35e-06 |
7 |
5.12e-09 |
7.17e-08 |
|
73 |
103 |
7.63e-08 |
1.28e-06 |
3 |
2.19e-09 |
6.95e-08 |
|
74 |
756 |
5.60e-07 |
7.17e-07 |
15 |
1.10e-08 |
5.85e-08 |
|
75 |
255 |
1.89e-07 |
5.28e-07 |
3 |
2.19e-09 |
5.63e-08 |
|
76 |
51 |
3.78e-08 |
4.90e-07 |
8 |
5.85e-09 |
5.05e-08 |
|
77 |
45 |
3.33e-08 |
4.56e-07 |
0 |
0.00e+00 |
5.05e-08 |
|
78 |
354 |
2.62e-07 |
1.94e-07 |
9 |
6.58e-09 |
4.39e-08 |
|
79 |
188 |
1.39e-07 |
5.48e-08 |
19 |
1.39e-08 |
3.00e-08 |
|
80 |
64 |
4.74e-08 |
7.41e-09 |
19 |
1.39e-08 |
1.61e-08 |
|
81 |
10 |
7.41e-09 |
0.00e+00 |
21 |
1.54e-08 |
7.32e-10 |
|
82 |
0 |
0.00e+00 |
0.00e+00 |
1 |
7.32e-10 |
0.00e+00 |
|
83 |
0 |
0.00e+00 |
0.00e+00 |
0 |
0.00e+00 |
0.00e+00 |
|
84 |
0 |
0.00e+00 |
0.00e+00 |
0 |
0.00e+00 |
0.00e+00 |
|
85 |
0 |
0.00e+00 |
0.00e+00 |
0 |
0.00e+00 |
0.00e+00 |
|
86 |
0 |
0.00e+00 |
0.00e+00 |
0 |
0.00e+00 |
0.00e+00 |
|
87 |
0 |
0.00e+00 |
0.00e+00 |
0 |
0.00e+00 |
0.00e+00 |
|
88 |
0 |
0.00e+00 |
0.00e+00 |
0 |
0.00e+00 |
0.00e+00 |
|
89 |
0 |
0.00e+00 |
0.00e+00 |
0 |
0.00e+00 |
0.00e+00 |
|
Total |
1349517312 |
1.00e+00 |
1366818816 |
1.00e+00 |
Table 1: Score distribution for FSA and ANN organisms
6. The genetic algorithm
The genetic algorithm we used is a reasonably standard one (Goldberg 1989), though to our knowledge GA’s are rarely attempted on bit strings of this length. We begin with a population of 65,536 bit strings of random bits, each of which is either 448 or 453 bits (depending on the ant representation to be used). Each bit string is decoded into either an FSA or an ANN, and all 65,536 ants are executed for 200 time units (in parallel) on separate copies of the trail. At the end of each generation all of the ants are scored as to their success on the trail. Those ants scoring among the highest of their generation (between 1% and 10% selection fraction) are selected for breeding, and all others are discarded. Ties are broken arbitrarily. Then the new generation is produced by the following procedure.
a) Mating: 65,536 pairs of the bit strings are chosen at random (with replacement) from the selected fraction. No preference is given to those ants scoring higher than others within the selected fraction.
b) Recombination: From each pair a single bit string is constructed by random crossover. The crossover probability is typically between 0.5% and 1.0% per bit, so the mean number of crossovers per ant per generation is 2.25 to 4.5. Crossovers are performed without regard to the boundaries of semantic units in the bit string (e.g. state fields in the FSA genome,or weight fields in the ANN genome).
c) Point mutation: The recombined string is mutated by random bit-flip operations, again at a rate anywhere from 0.1% to 1% per bit. The mean number of mutations is thus also 0.225 to 2.25 per ant per generation.
Numerous sensitivity studies were performed to determine that the selection, mutation, and recombination parameters were reasonable and effective. These rates are in line with those reported in (Goldberg 1988) for other genetic algorithms. The qualitative character of the results are extremely robust over wide variations of the evolutionary parameters.
7. Results
Figure 7 shows Hercules, the highest-scoring ant in Generation 0 of one run of Genesys with the FSA representation. Since no evolution has taken place, it is just the highest scorer in a particular random sample of 65,536 FSAs. The diagram shown here has been simplified in two ways in order to expose the underlying algorithm: (a) states and transitions that are coded for by the ant’s chromosome but are unreachable on the John Muir Trail have been removed; (b) the result was then processed by a state-minimization procedure to remove redundant logic; and (c) the states were renumbered from 0 to 16.
Hercules gets a score of 58 on the task. It has great difficulty getting around the first three right turns of the trail. It arrives at those turns in state 7 and taking 10 state transitions in each case (1,13,14,15,16,14,15,16,14) before leaving in state 9. It has even greater difficulty making the left turn at trail step 32, requiring two executions of the cycle (8,1,2,3,4,5,6,7) before using the right turn sequence (1,13,...) above. On the straight-away segments of the trail it takes two transitions per step around the 7-8 loop in the diagram, which is a very time-inefficient way to travel. Curiously, Hercules can make a left turn where the corner square is missing, as at step 42 on the trail, more efficiently than it can when the corner square is present! Arriving at the corner in state 8, one trip around the cycle (1,2,3,4,5,6,7,8) makes the turn. Hercules runs out of time when it gets to the double gap at trail step 58, though it would not make it across the gap even if it had more time.
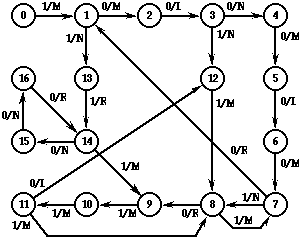
Figure 7: Hercules, the champion FSA in generation 0, which scores 58.
In Figure 8 we show Joyner, an FSA-ant that is the product of 200 generations of evolution starting from the population of 65,536 of which the FSA in Figure 7 was the champion. The evolution was conducted with a mutation rate of 0.5%/bit, a recombination rate of 0.5%/bit, and a selection fraction of 1%/generation. Its logic has been simplified in the same way Hercules’ was. Although Joyner is descended from the same population that included Hercules, there is no reason to believe Hercules is actually a genetic ancestor of Joyner, and in fact it is rather unlikely.
Joyner gets a perfect score of 89, demonstrating that it is indeed possible to traverse this trail in 200 steps. In fact, Joyner takes exactly 200 time steps to finish the trail. Since the scoring function does not give any extra credit for reaching the end sooner, there is no selective pressure for any further improvement in performance.
There are a number of fascinating features we can observe in Joyner’s logic. First, it traverses the straightaway portions of the trail by staying in state 0 or in state 9, thereby taking one unit of time per trail step rather than two. Second, it makes a right turn from state 0 using the (1,12,0) cycle, a far more efficient mechanism than Hercules used, though not optimal. The left turn at trail step 32 is accomplished by three right turns. We placed three right turns in the trail before the first left turn precisely to see if there would be an evolutionary bias toward more efficient right-turning. In this case apparently, there was.
The state sequence (9,10,11) is extremely versatile. It is used in four critical places along the trail: at step 42 (left turn with missing corner), at steps 58 and 74 (straightaway double gap) and at step 64 (forward right knight’s jump). Likewise, the sequences (12,7,8,3,4,0) and (6,4,0) are used repeatedly to traverse the "stepping stone" part of the trail from step 78 to 89. Such efficient logic seems exquisitely adapted to the features of this particular trail, and suggests that evolution has had the effect of "compiling" knowledge of this environment into the structure of the organism.
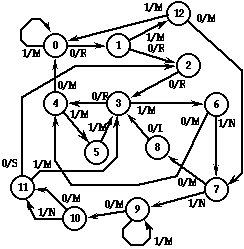
Figure 8: Joyner, the champion FSA in generation 200, which scores 89.
In Figures 9 and 10 we chart the evolutionary progress of the entire population in the tracker task, one chart with FSA ants and one for ANN ants. These are runs typical of many we have made, and are chosen for presentation here because their parameters are identical. In both cases the mutation and recombination rates are 1% per bit per generation, and the selection fraction is 5% per generation. Both runs evolve a population of 65536 for 100 generations. Each took about one hour on a 16K-processor Connection Machine (CM2).
Figure 9 is a graph of the progress of an evolution with FSA ants. The horizontal axis is the generation number, and the vertical axis is the score on the tracker task. Four population statistics are plotted as a function of generation:
(a) the maximum score achieved by any ant in the generation
(b) the mode (most frequent) score
(c) the mean score
(d) the standard deviation of the scores
Initially the mean score was somewhere around 3, but the maximum score was 58, consistent with the statistics given in Section 6. After 15 generations of selection the maximum score is already in the 80s, and by generation 52 perfect-scoring ants are always present in the population, and are the most common score by generation 70. However, the mean score never approaches the maximum score, hovering around 56 for the last 75 generations, and there is always a high standard deviation. The high variance and the great difference between the mean and the max scores is, we have learned, a consequence of the relatively high mutation rate of 1%/bit. We can get similar results with a mutation rate two orders of magnitude smaller, but then the mean score reaches the 80s. With a high mutation rate shown here, a large fraction of successful parents have offspring that are destroyed by mutation and hence bring down the average score.

Figure 9: Evolution of FSA ants
Figure 10 is a similar graph except that the ants were represented as artificial neural nets. All evolution parameters are the same as in Figure 9. We see similar features in Figure 10, i.e. the maximum score starts low (this time at 46) and quickly reaches the 80s (by generation 18). It then takes a long time to reach 89 (generation 94). As in Figure 9, there is a large gap between the maximum score and the mean score, and for the same reasons. Comparing Figure 9 to Figure 10 we see that evolution proceeds somewhat more slowly in the ANN representation than in the FSA representation, for reasons unknown. This result was consistent over hundreds of executions with many different parameters.

Figure 10: Evolution in neural net ants.
8. Conclusions
It is clear we can now answer some of the questions posed at the beginning. We can indeed evolve program texts, not just parameters to programs. The feasibility of genetic algorithms does indeed scale up to at least 450-bit strings (at least when a population of 65536 can be maintained). And recurrent ANNs can be produced by genetic algorithm as an alternative to learning mechanisms. Much work remains, however on these questions, and on the more fundamental questions of (a) the representation of organisms by programs, and (b) the use of genetic algorithms over programs to illustrate principles of natural evolution and resolve outstanding questions about it. One such follow-on effort is currently in progress at UCLA, as reported in (Collins and Jefferson 1990)
Bibliography
To the reviewer: additional citations to Holland, Goldberg, Davis, Koza, and Hinton (and no doubt others) will be added.
Collins, Robert and David Jefferson, (1990) AntFarm. Submitted to Artificial Life II, Langton, C. G., Farmer, D., Rasmussen, S. and Taylor, C. (eds.), Addison-Wesley
Ellman, J. L. (1988) Finding Structure in Time. CRL Tech. Rep. 8801. Center for Research in Language. University of California, San Diego
Goldberg, D. E. (1989) Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley
Goldberg, D. E. and J. H. Holland (eds.) (1988). Machine Learning. Vol. 3, Nos. 2-3, Special Issue on Genetic Algorithms, Kluwer Academic Publishers
Hillis, W. D. (1987) The Connection Machine. MIT Press, Cambridge, Mass.
Holland, John (1975), Adaptation in Natural and Artificial Systems, The Universtiy of Michigan Press
Holldobler, Bert and Wilson, Edward O., (1990) The Ants, Harvard University Press
Langton, C. G. (ed.) (1989). Artificial Life. Addison-Wesley
Montana, D. J. and Davis, L. (1989) Training Feedforward Neural Networks Using Genetic Algorithms, Proceedings of 11th International Joint Conference on Artificial Intelligence (IJCAI-89), Detroit, MI.
Pearlmutter, B. A. (1989). Learning state space trajectories in recurrent neural networks, in D. Touretzky, G. Hinton, and T. Sejnowski (eds.) Proceedings of the 1988 Connectionist Models Summer School, Morgan Kaufmann
Rumelhart, D. e. and J. L. McClelland (eds.) (1986). Parallel Distributed Processing, Vols. 1 and 2. Bradford Books/MIT Press.
Servan-Schreiber, D., A. Cleeremans, and J. L. McClelland. (1989). Learning Sequential Structure in Simple Recurrent Networks. In D. S. Touretzky (ed.) Advances in Neural Information Processing Systems 1, pp. 643-652